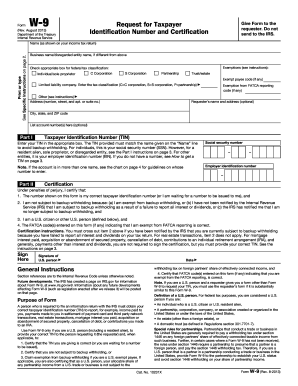SF 1034 1987-2025 free printable template

Standard Form 1034 Revised October 1987 Department of the Treasury 1 TFM 4-2000 1034-122 VOUCHER NO. PUBLIC VOUCHER FOR PURCHASES AND SERVICES OTHER THAN PERSONAL U*S* DEPARTMENT BUREAU OR ESTABLISHMENT AND LOCATION DATE VOUCHER PREPARED SCHEDULE NO. CONTRACT NUMBER AND DATE PAID BY REQUISITION NUMBER AND DATE PAYEE S NAME AND ADDRESS DATE INVOICE RECEIVED DISCOUNT TERMS PAYEE S ACCOUNT NUMBER SHIPPED FROM NUMBER AND DATE OF ORDER TO DATE OF DELIVERY OR SERVICE WEIGHT ARTICLES OR SERVICES...

How to fill out sf1034 form

How to fill out SF 1034

1. Download the SF 1034 form from the official government website.
2. Enter the date at the top of the form.
3. Fill in the name of the organization requesting the payment.
4. Provide the address and contact information for the organization.
5. Enter the specific details of the payment, including the amount and purpose.
6. Include relevant data such as invoice numbers or contract information.
7. Sign and date the form at the bottom.
8. Submit the completed form to the designated payment authority.

Who needs SF 1034?

1. Government agencies that require reimbursement or payment processing.
2. Contractors or vendors providing services to government entities.
3. Organizations that manage funds on behalf of government projects.

Video instructions and help with filling out and completing sf1034 fillable

Instructions and Help about sf1034 form

People Also Ask about 1034 public

What is the difference between IRS and Department of Treasury?

The IRS is a bureau of the Department of the Treasury and one of the world's most efficient tax administrators. In fiscal year 2020, the IRS collected almost $3.5 trillion in revenue and processed more than 240 million tax returns. The IRS spent just 35 cents for each $100 it collected in FY 2020.

What are 3 things the Department of Treasury does?

Government accounting, cash, and debt management. Promulgation and enforcement of tax and tariff laws. Assessment and collection of internal revenue. Production of coin and currency.

What does a treasury department do?

The Department of the Treasury operates and maintains systems that are critical to the nation's financial infrastructure, such as the production of coin and currency, the disbursement of payments to the American public, revenue collection, and the borrowing of funds necessary to run the federal government.

How do I know if I owe the Department of Treasury?

The TOP Interactive Voice Response (IVR) system at 800-304-3107 can provide an automated message on who to call for your specific debt.

Where is U.S. Treasury Department located?

The Treasury Building is located at 1500 Pennsylvania Avenue, NW, in Washington, D.C. was designated a National Historic Landmark in 1972. This view is taken from the north. In the distance is the Washington Monument.

What is the Department of Treasury used for?

The Department of the Treasury operates and maintains systems that are critical to the nation's financial infrastructure, such as the production of coin and currency, the disbursement of payments to the American public, revenue collection, and the borrowing of funds necessary to run the federal government.

For pdfFiller’s FAQs

What is treasury department?

The Treasury Department is a federal government agency that is responsible for managing the United States government's financial assets, issuing public debt, and producing coin and currency. The Treasury Department also serves as the government's fiscal agent, collecting taxes and other payments, managing government accounts, and providing services to other government agencies.

Who is required to file treasury department?

The Treasury Department requires certain businesses and individuals to file reports on various forms, including Form 8300, Form TD F 90-22.1, and Form FinCen 114. These reports are required for certain transactions related to money laundering, terrorist financing, and other financial crimes.

What is the purpose of treasury department?

The purpose of the treasury department is to manage the finances of the government and ensure the soundness of the financial system. The department is responsible for collecting taxes, managing the public debt, issuing currency, supervising national banks, and providing economic and financial advice to the President and Congress.

How to fill out treasury department?

Filling out the treasury department involves the process of hiring and staffing individuals for various positions within the department. Here are the steps to fill out the treasury department: 1. Identify the positions needed: Determine the roles and positions required to run the treasury department effectively. This may include positions such as treasurer, financial analyst, cash management specialist, risk management officer, accountant, and tax specialist. 2. Define job descriptions: Create detailed job descriptions that outline the responsibilities, qualifications, and experience required for each position. These job descriptions will help attract the right candidates and assist in evaluating applicants. 3. Advertise the positions: Publicize job vacancies through various channels such as online job portals, industry-specific websites, professional associations, careers pages, and social media platforms. Specify necessary qualifications, application deadlines, and provide contact information for interested applicants. 4. Review applications: Screen the received applications to shortlist candidates who meet the qualifications outlined in the job descriptions. Consider their experience, education, skills, and other relevant criteria specified in the job posting. 5. Conduct interviews: Schedule interviews with the shortlisted candidates to assess their suitability for the positions. These interviews may involve a panel of interviewers including representatives from the treasury department and other relevant stakeholders within the organization. 6. Assess skills and compatibility: During the interview process, evaluate candidates' technical skills, industry knowledge, problem-solving abilities, and cultural fit within the organization. This helps ensure that the selected individuals can effectively contribute to the department's goals and work well with existing team members. 7. Perform background checks: Conduct background checks on the final candidates to verify their qualifications, experience, and references provided in their application. This step helps to confirm the applicants' credibility and reliability. 8. Make job offers: Based on the evaluation of candidates and their background checks, extend job offers to the selected individuals. Clearly communicate the terms and conditions of employment, compensation packages, and any other relevant details. 9. Onboarding and training: Once the candidates accept the job offers, initiate the onboarding process. Provide them with the necessary paperwork, introduce them to colleagues, and ensure they receive appropriate training to familiarize themselves with their roles, responsibilities, and the overall functioning of the treasury department. 10. Monitor and support: After the new hires join the treasury department, consistently monitor their performance and provide support as needed. Conduct periodic evaluations and address any concerns or opportunities for growth.

What information must be reported on treasury department?

There are several types of information that must be reported to the Treasury Department. The specific details may vary depending on the specific reporting requirements and regulations, but some common information that needs to be reported includes: 1. Financial transactions: The Treasury Department requires reporting of various financial transactions, such as receipts, disbursements, investments, loans, and grants. 2. Cash balances: Organizations must report their cash balances, including details of the accounts held, the amount of cash, and any changes in cash balances over a given period. 3. Debt and borrowing: Entities that have borrowed money or issued debt securities are required to report details of the debt obligations, including the principal amounts, interest rates, maturity dates, and any covenants or guarantees associated with the debt. 4. Foreign transactions: Reporting of foreign transactions and financial activities is a crucial requirement for individuals, organizations, and businesses engaged in international trade or financial transactions. This may include reporting of foreign bank accounts, investments, or transactions with foreign entities. 5. Tax-related information: The Treasury Department requires reporting of various tax-related information, such as income, deductions, credits, and other financial details necessary to compute and report taxes owed. 6. Money laundering and anti-terrorism: Financial institutions are required to report suspicious transactions or activities that may indicate money laundering, terrorist financing, or other illegal activities. These reports help in preventing and combating financial crimes. 7. Sanctions compliance: Organizations engaged in international transactions need to comply with various economic sanctions and embargo programs. Reporting to the Treasury Department is necessary to ensure compliance with these regulations. 8. Corporate governance and compliance: Some reporting requirements by the Treasury Department pertain to corporate governance and compliance matters, including details of board members, executive compensation, related-party transactions, and other disclosures required by law or regulatory bodies. These are just some examples of the information that may need to be reported to the Treasury Department. The specific reporting requirements can vary based on the nature and type of the organization, financial activities, and local regulations.

How can I modify sf1034 pdf without leaving Google Drive?

It is possible to significantly enhance your document management and form preparation by combining pdfFiller with Google Docs. This will allow you to generate papers, amend them, and sign them straight from your Google Drive. Use the add-on to convert your sf 1034 instructions into a dynamic fillable form that can be managed and signed using any internet-connected device.

How can I send standard form 1034 fillable to be eSigned by others?

When you're ready to share your 1034, you can swiftly email it to others and receive the eSigned document back. You may send your PDF through email, fax, text message, or USPS mail, or you can notarize it online. All of this may be done without ever leaving your account.

How do I edit sf 1034 form pdf straight from my smartphone?

The best way to make changes to documents on a mobile device is to use pdfFiller's apps for iOS and Android. You may get them from the Apple Store and Google Play. Learn more about the apps here. To start editing government form 1034, you need to install and log in to the app.

What is SF 1034?

SF 1034, or the Public Voucher for Payments Under Federal Programs, is a form used by federal agencies to request reimbursement for expenses incurred in providing goods or services.

Who is required to file SF 1034?

Federal agencies and certain organizations that receive federal funds are required to file SF 1034 to request reimbursement.

How to fill out SF 1034?

To fill out SF 1034, the filer must complete sections including the payee information, account details, description of the services or goods provided, cost breakdown, and certification of the expenses.

What is the purpose of SF 1034?

The purpose of SF 1034 is to provide a standardized method for federal agencies to request payment for expenses, ensuring accountability and proper documentation of federal funds.

What information must be reported on SF 1034?

Information that must be reported on SF 1034 includes the payee's name and address, the federal program or project number, the amount requested, a description of the services provided, and supporting documentation of expenses.